题目内容
3.定义:如果代数式a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与a2x2+b2x+c2(a2≠0,a2,b2,c2是常数),满足a1+a2=0,b1+b2=0,c1+c2=0,则称两个代数式互为”牛郎织女式”(1)写出-x2+2x-3的“牛郎织女式”;
(2)若-x2-18mx-3与x2-2nx+n互为“牛郎织女式”,求(mn)2015的值;
(3)无论x取何值时,代数式x2-2x+a的值总大于其“牛郎织女式”的值,求a的取值范围.
分析 (1)根据定义即可求出-x2+2x-3的“牛郎织女式”;
(2)根据定义求出m与n的值,代入原式求值即可;
(3)利用作差法即可求出a的范围.
解答 解:(1)设-x2+2x-3的“牛郎织女式”为ax2+bx+c
由题意可知:a=1,b=-2,c=3,
∴-x2+2x-3的“牛郎织女式”为x2-2x+3;
(2)由题意可知:-18m-2n=0,-3+n=0,
解得:m=-$\frac{1}{3}$,n=3,
∴原式=(-1)2015=-1;
(3)x2-2x+a的“牛郎织女式”为-x2+2x-a,
∴由题意可知:x2-2x+a>-x2+2x-a对于任何x都成立,
∴x2-2x+a-(-x2+2x-a)>0,
∴a>-x2+2x,
∴a>-(x-1)2+1对于任何的x都成立,
∵-(x-1)2+1的最大值为1,
∴a>1,
点评 本题考查学生的阅读理解能力,涉及相反数的性质,解方程,代入求值,不等式的解法,配方法求值最值等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.方程组$\left\{\begin{array}{l}{{x}^{2}-y={z}^{2}}\\{{y}^{2}-z={x}^{2}}\\{{z}^{2}-x={y}^{2}}\end{array}\right.$ 的解(x,y,z)有( )
| A. | 1组 | B. | 3组 | C. | 4组 | D. | 7组 |
13.下列各式计算正确的是( )
| A. | 2a+3b=5ab | B. | 3a2+2a3=5a5 | C. | 6ab-ab=5ab | D. | 5+a=5a |
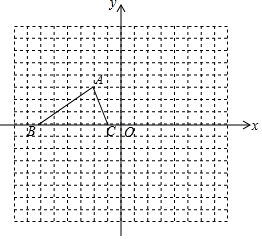 如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).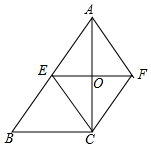 如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.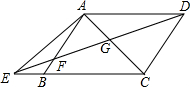 如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.
如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.