Question

P为正方形ABCD内一点，若PA：PB：PC=1：2：3，则∠APB的度数为

1. A.
   120°
2. B.
   135°
3. C.
   150°
4. D.
   以上都不对

Answer 1

B
分析：三条已知的线段PA、PB、PC具有一个共公顶点，且它们不能构成三角形，但是当把△ABP按顺时针方向旋转90°后，即会出现等腰直角三角形，于是PA旋转后的线段与PC构成了一个新的三角形．
解答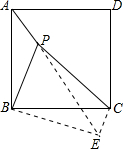：解：将△ABP绕点B顺时针方向旋转90°得△CBE，如图．
则△ABP≌△CBE，且PB⊥EB
设PA=a，PB=2a，PC=3a
∴PB=EB=2a，
∴△PBE是等腰直角三角形，∠BPE=∠BEP=45°，PE=2a
在△PEC中，∵PC²=9a²，PE²+EC²=9a²
∴PC²=PE²+EC²
∴∠PEC=90°
故∠APB=∠CEB=90°+45°=135°
故选B．
点评：辅助线作法是一种常用作法．这种方法在解决等腰三角形、等边三角形、正方形的问题中最为多见．