题目内容
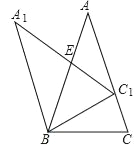
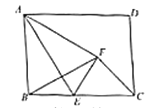
【题目】如图,矩形![]() 中
中![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落到
落到![]() 处,连接
处,连接![]() ,
,![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为__________.
的长为__________.
【答案】![]() 或
或![]() 或12
或12
【解析】
当![]() 为等腰三角形时,有三种情况,需分别讨论:①:
为等腰三角形时,有三种情况,需分别讨论:①:![]() ;②:
;②:![]() ;③:
;③:![]() .
.
①:![]() ;首先,因为折叠,
;首先,因为折叠,![]() ,
,![]() ,则
,则![]() ,另因
,另因![]() ,则
,则![]() ,可证得
,可证得![]() ,则
,则![]() ,因此只要求出
,因此只要求出![]() 的值,即可求出
的值,即可求出![]() 的值,过点
的值,过点![]() 朝
朝![]() 作垂线,垂足为
作垂线,垂足为![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,由矩形的性质可知,
,由矩形的性质可知,![]() ,
,![]() ,利用等腰三角形三线合一的性质,可知
,利用等腰三角形三线合一的性质,可知![]() ,则在
,则在![]() 中,
中,![]() ,则
,则![]() ,再利用勾股定理,在
,再利用勾股定理,在![]() 中,有
中,有![]() ,由于
,由于![]() ,则
,则![]() ,
,![]() ,解得
,解得![]() .
.
②:![]() ,若
,若![]() 与
与![]() 交于点
交于点![]() ,首先因为折叠,可知
,首先因为折叠,可知![]() 为
为![]() 的垂直平分线,不难证明出
的垂直平分线,不难证明出![]() ,则
,则![]() ,则若能求得
,则若能求得![]() 、
、![]() 的值,则此题便得以解答.因
的值,则此题便得以解答.因![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,则
,则![]() ,得
,得![]() .
.
③:![]() ,因
,因![]() ,且因为折叠
,且因为折叠![]() ,则
,则![]() 为线段
为线段![]() 的垂直平分线,所以点
的垂直平分线,所以点![]() 与点
与点![]() 重合,
重合,![]() .
.

故答案为:![]() 或
或![]() 或12.
或12.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目