题目内容
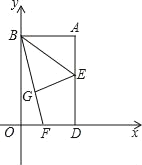
【题目】如图,□![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,且AE∥BD,BE∥AC,OE = CD.
,且AE∥BD,BE∥AC,OE = CD.
(1)求证:四边形ABCD是菱形;
(2)若AD = 2,则当四边形ABCD的形状是_______________时,四边形![]() 的面积取得最大值是_________________.
的面积取得最大值是_________________.

【答案】(1)详见解析;(2)正方形;2.
【解析】
(1)判定四边形![]() 是矩形,根据矩形的性质有
是矩形,根据矩形的性质有![]() ,即可证明
,即可证明
四边形ABCD是菱形;
(2)由(1)知四边形![]() 是矩形,
是矩形,![]() 所以
所以![]()
![]()
![]() 即可得出答案.
即可得出答案.
(1)证明:∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴平行四边形![]() 是矩形.
是矩形.
∴![]() .
.
∴![]() .
.
∴平行四边形![]() 是菱形.
是菱形.
(2)由(1)知四边形![]() 是矩形,
是矩形,
![]()
所以![]()
![]()
![]()
![]()
![]()
当![]() 时,矩形的AOBE的面积有最大值,最大值为2,
时,矩形的AOBE的面积有最大值,最大值为2,
![]()
![]()
四边形ABCD是菱形,
![]() 四边形ABCD是正方形.
四边形ABCD是正方形.
故答案为:正方形; 2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 | 购买数量(件 | 购买总费用(元 | |
A | B | ||
第一次 | 2 | 1 | 55 |
第二次 | 1 | 3 | 65 |
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.