��Ŀ����
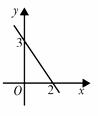
��ͼ��A��0��1����M��3��2����N��4��4��������P�ӵ�A��������y����ÿ��1����λ�����ٶ������ƶ����ҹ���P��ֱ��l��y=��x+bҲ��֮�ƶ������ƶ�ʱ��Ϊt�룮
��1����t=2ʱ����AP= ,��ʱ��P�������� ��
��2����t=3ʱ�������P��ֱ��l��y=��x+b�Ľ���ʽ��
��3����ֱ��l��y=��x+b�Ӿ�����M����Nʱ�����ʱ��P�����ƶ������룿
��4����Q��x��ʱ����S��ONQ=8ʱ����ֱ��д����Q�������� ��

(1) 2, (0,3)
��2��ֱ�� ��y���ڵ�P��0��b����
��y���ڵ�P��0��b����
�����⣬��b>0��t��0��b=1+t ��t=3ʱ��b=4��
��3����ֱ�� ��M��3,2��ʱ
��M��3,2��ʱ ���b=5 5=1+t1 ��t1=4
���b=5 5=1+t1 ��t1=4
��ֱ�� ��N��4,4��ʱ
��N��4,4��ʱ ��� b=8 8=1+ t2 ��t2=7
��� b=8 8=1+ t2 ��t2=7
��t2��t1��������������.����
��4����������������������

��ϰ��ϵ�д�
�����Ŀ

 ��2=3 B����
��2=3 B���� =��3��C����
=��3��C���� ��2=3 D��
��2=3 D�� =��3
=��3
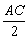 �ij�Ϊ�뾶��Բ����Rt��ABC��ȥ�������Σ���ʣ�ࣨ��Ӱ�����ֵ����Ϊ
�ij�Ϊ�뾶��Բ����Rt��ABC��ȥ�������Σ���ʣ�ࣨ��Ӱ�����ֵ����Ϊ 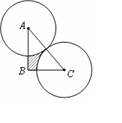
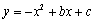 ����1,4���루4,-5�����㣬��.��һֱ��
����1,4���루4,-5�����㣬��.��һֱ��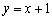 �ཻ��A��C���㣬
�ཻ��A��C���㣬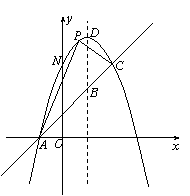
 ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ�� ʱ��
ʱ��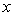 ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��