题目内容
已知：如图，在四边形ABCD中，∠C=60°，∠DAB=135°，BC=8，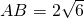
，求DC的长．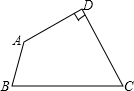
解：如图，过B作BE∥AD交CD于E，过A作AF⊥BE于F∴∠BEC=∠ADC=90°，∠ABE=180°-∠A=45°，AF=DE，
Rt△BEC中，CE=BC•cos∠C=8×
=4Rt△ABF中，AF=AB•sin∠ABF=2
，∴DC=4+2
分析：过B作BE∥AD交CD于E，过A作AF⊥BE于F，由已知条件得AF=DE，在直角三角形中，利用三角函数，求得CE，AF，从而求得CD的长即可．
点评：本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．
练习册系列答案
相关题目
39、已知：如图，在四边形ABCD中，AB=DC，AD=BC，点E在BC上，点F在AD上，AF=CE，EF与对角线BD相交于点O．求证：O是BD的中点．
已知：如图，在四边形ABCD中，AD∥BC，AC⊥BC，点E、F分别是边AB、CD的中点，AF=CE．求证：AD=BC．
已知：如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2．
已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．