题目内容
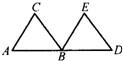
 如右下图,等边△ABC外一点P到三边距离分别为h1,h2,h3,且h3+h2-h1=3,其中PD=h3,PE=h2,PF=h1.则△ABC的面积S△ABC=
如右下图,等边△ABC外一点P到三边距离分别为h1,h2,h3,且h3+h2-h1=3,其中PD=h3,PE=h2,PF=h1.则△ABC的面积S△ABC=
- A.2

- B.3

- C.10

- D.12

B
分析:分析题知要求等边三角形的面积先求出边长,由图中几何关系和已知条件可求出三角形的高从而求出三角形的边长.
解答:∵△ABC是等边三角形.
设△ABC的边长是x,S△ABC= .
.
而S△ABC=S△ABP+S△ACP-S△BCP= h3•x+
h3•x+ h2•x-
h2•x- h3•x=
h3•x= x(h3+h2-h1),
x(h3+h2-h1),
h3+h2-h1=3;
∴ =
= x
x
∴x=2 .
.
∴S△ABC= (2
(2 )2=3
)2=3 .
.
故选B.
点评:此题主要考查了等边三角形的性质,三边的高相等的特点来解题.
分析:分析题知要求等边三角形的面积先求出边长,由图中几何关系和已知条件可求出三角形的高从而求出三角形的边长.
解答:∵△ABC是等边三角形.
设△ABC的边长是x,S△ABC=
 .
.而S△ABC=S△ABP+S△ACP-S△BCP=
 h3•x+
h3•x+ h2•x-
h2•x- h3•x=
h3•x= x(h3+h2-h1),
x(h3+h2-h1),h3+h2-h1=3;
∴
 =
= x
x∴x=2
 .
.∴S△ABC=
 (2
(2 )2=3
)2=3 .
.故选B.
点评:此题主要考查了等边三角形的性质,三边的高相等的特点来解题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目