题目内容
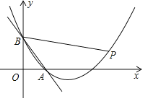
【题目】如图,直线![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,过
两点,过![]() ,
,![]() 两点的抛物线与
两点的抛物线与![]() 轴的另一交点为
轴的另一交点为![]() ,
,![]() 为抛物线上的一动点,当
为抛物线上的一动点,当![]() 时,
时,![]() 点的坐标为________.
点的坐标为________.
【答案】![]()
【解析】
先求出二次函数的解析式,然后过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,可得∠CBA=45°,设点C坐标为(a,0),利用面积公式求出a值,然后得出点C坐标,根据BC⊥BD,BO⊥CD,可得△BCO∽DCB,进而得出![]() ,求出点D的坐标,然后求出直线BD的解析式,与二次函数解析式联立求出点P的坐标.
,求出点D的坐标,然后求出直线BD的解析式,与二次函数解析式联立求出点P的坐标.
设二次函数的解析式为y=ax2+bx+c,
则 ,
,
解得: ,
,
二次函数的解析式为:y=![]() x2-
x2-![]() x+2,
x+2,
过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,则有∠CBA=45°,
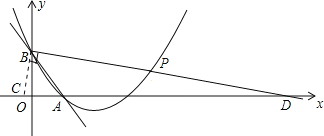
设点C坐标为(a,0)(a<0),
∵S△ABC=![]() BCABsin∠ABC=
BCABsin∠ABC=![]() ACBO,
ACBO,
∴![]() ,
,
整理得:3a2-16a-12=0,
解得:a=-![]() 或a=6(不合题意,舍去),
或a=6(不合题意,舍去),
∴点C(-![]() ,0),
,0),
∵BC⊥BD,BO⊥CD,
∴△BCO∽DCB,
则有![]() ,
,
即BC2=COCD,
∴![]() ,
,
解得:OD=6,
即点D(6,0),
∵B(0,2),
∴设直线BD的解析式为y=kx+m,
代入得:![]() ,
,
解得: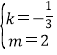 ,
,
∴直线BD的解析式为y=-![]() x+2,
x+2,
与二次函数的解析式联立得:
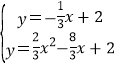 ,
,
解得:![]() ,
, ,
,
即点P的坐标为(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目