题目内容
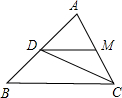
如图,在△ABC中,M是AC的中点,P,Q为边BC的三等分点.若BM与AP,AQ分别交于D,E两点,则BD,DE,EM三条线段的长度比等于( )

| A.3:2:1 | B.4:2:1 | C.5:3:2 | D.5:2:1 |

过A作AF∥BC交BM延长线于F,设BC=3a
则BP=PQ=QC=a;
∵AM=CM,AF∥BC,
∴AF:BC=AM:CM=1,
∴AF=BC=3a,
∴BD:DF=BP:AF=1:3,
∴BD=
,
同理可得:
BE=
,BM=
;
∴DE=BE-BD=
,EM=BM-BE=
,
∴BF:FG:GE
=
:
:
=5:3:2;
故选C.

则BP=PQ=QC=a;
∵AM=CM,AF∥BC,
∴AF:BC=AM:CM=1,
∴AF=BC=3a,
∴BD:DF=BP:AF=1:3,
∴BD=
| BF |
| 4 |
同理可得:
BE=
| 2BF |
| 5 |
| BF |
| 2 |
∴DE=BE-BD=
| 3BF |
| 20 |
| BF |
| 10 |
∴BF:FG:GE
=
| 1 |
| 4 |
| 3 |
| 20 |
| 1 |
| 10 |
=5:3:2;
故选C.


练习册系列答案
相关题目