题目内容
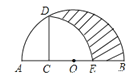
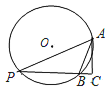
【题目】如图，
的半径为2，弦
，点P为优弧AB上一动点，
，交直线PB于点C，则
的最大面积是
A.
B.1C.2D.
【答案】B
【解析】
连接OA、OB，如图1，由
可判断
为等边三角形，则
，根据圆周角定理得
，由于
，所以
，因为
，则要使
的最大面积，点C到AB的距离要最大；由
，可根据圆周角定理判断点C在
上，如图2，于是当点C在半圆的中点时，点C到AB的距离最大，此时为等腰直角三角形，从而得到的最大面积．
解：连接OA、OB，如图1，
，，
为等边三角形，
，
，
，要使的最大面积，则点C到AB的距离最大，
作的外接圆D，如图2，连接CD，
，点C在上，AB是的直径，
当点C半圆的中点时，点C到AB的距离最大，此时等腰直角三角形，
，
，
AB
CD
，
的最大面积为1．
故选B．
练习册系列答案
寒假学与练系列答案
相关题目
