题目内容
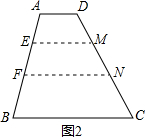
如图(11),梯形ABCD,AB∥CD ,AB=2cm,且∠OAB=30°,∠OBA=45°,梯形ABCD内部的⊙O分别切四边于E,F,M,N,

1.求出⊙O的半径OM的长度
2.求出梯形ABCD的周长.
1.∵⊙O切AB于M
∴OM⊥AB ……………………………………………………………………1分
又∵∠OAB=30°,∠OBA=45°
∴AM=OM·cot30°=![]() OM
OM
BM=OM·cot45°=OM……………………………………………………3分
∵AM+BM=AB
∴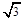 OM+OM=2 则OM=
OM+OM=2 则OM=![]() =
=![]() ………………………………5分
………………………………5分
2.作DG⊥AB,

∵⊙O分别切AB,AD于F,M,且∠OAB=30°
∴∠DAB=60°……………………………………………………………………7分
又∵OM=![]() 则DG=BC=2(
则DG=BC=2(![]() )
)
∴AD=![]() =2(
=2(![]() )·
)·![]() =
=![]() …………8分
…………8分
AG=![]() ……………………………………………9分
……………………………………………9分
∴ C梯形ABCD=2AB-AG+AD+BC=![]() ……………………………10分
……………………………10分
解析:(1)利用三角函数算出OM与AB的关系,得出结果;
(2)利用梯形的高等于圆的直径得出高的大小,再根据外切得出∠DAB=60°和∠ABC=90°,然后利用三角函数求得AD、BC、AG的长度,最后利用周长公式求出结果。

练习册系列答案
相关题目
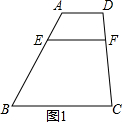 如图1,梯形ABCD中,AD∥BC,BC=a,AD=b,点E、F分别是两腰AB、CD上的点,且EF∥AD,设AE=d1、BE=d2,
如图1,梯形ABCD中,AD∥BC,BC=a,AD=b,点E、F分别是两腰AB、CD上的点,且EF∥AD,设AE=d1、BE=d2,