题目内容
 如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点D,交AB的延长线于点D,∠ACD=120°
如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点D,交AB的延长线于点D,∠ACD=120°
(1)求证:CA=CD
(2)求证:BD=OB
(1)证明:
∵CD切⊙O于点C,
∴∠OCD=90°,
∵∠ACD=120°,
∴∠ACO=30°,
∵AB是⊙O的直径,
∴OA=OC=OB,
∴∠A=30°,
∴∠D=30°,
∴CA=CD,
(2)∠A=30°,
∴∠COB=60°,
∵CO=BO,
∴△BOC是等边三角形,
∴OB=BC,
∵∠D=30°,
∴∠BCD=∠D=30°,
∴BD=BC,
∴BD=OB.
分析:(1)根据切线的性质,推出∠A,∠D的度数,即可推出结论;
(2)首先证明△BOC是等边三角形,所以可得OB=BC,再证明BD=BC即可.
点评:本题主要考查切线的性质,圆周角定理,等边三角形的判定和性质一等腰三角形的判定和性质,解题的关键在于求出∠D、∠A的度数
∵CD切⊙O于点C,

∴∠OCD=90°,
∵∠ACD=120°,
∴∠ACO=30°,
∵AB是⊙O的直径,
∴OA=OC=OB,
∴∠A=30°,
∴∠D=30°,
∴CA=CD,
(2)∠A=30°,
∴∠COB=60°,
∵CO=BO,
∴△BOC是等边三角形,
∴OB=BC,
∵∠D=30°,
∴∠BCD=∠D=30°,
∴BD=BC,
∴BD=OB.
分析:(1)根据切线的性质,推出∠A,∠D的度数,即可推出结论;
(2)首先证明△BOC是等边三角形,所以可得OB=BC,再证明BD=BC即可.
点评:本题主要考查切线的性质,圆周角定理,等边三角形的判定和性质一等腰三角形的判定和性质,解题的关键在于求出∠D、∠A的度数

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
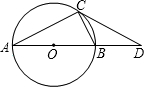 如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).
如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).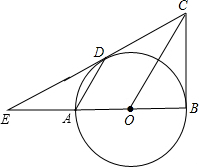 CD的延长线的交点.
CD的延长线的交点.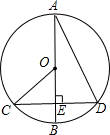 如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.
如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.

 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是