Question

【题目】如图，在矩形ABCD中，AD=4，∠DAC=30°，点P、E分别在AC、AD上，则PE+PD的最小值是（ ）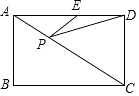

A.2
B.2
C.4
D.

Answer 1

【答案】B
【解析】作D关于直线AC的对称点D′，过D′作D′E⊥AD于E，

则D′E=PE+PD的最小值，

∵四边形ABCD是矩形，

∴∠ADC=90°，

∵AD=4，∠DAC=30°，

∴CD= ，

∵DD′⊥AC，

∴∠CDD′=30°，

∴∠ADD′=60°，

∴DD′=4，

∴D′E=2 ，

所以答案是：B．

【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识，掌握已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．