Question

【题目】某水产养殖户，一次性收购了小龙虾，计划养殖一段时间后再出售．已知每天放养的费用相同，放养天的总成本为万元；放养天的总成本为万元（总成本=放养总费用+收购成本）．

（1）设每天的放养费用是万元，收购成本为万元，求和的值；

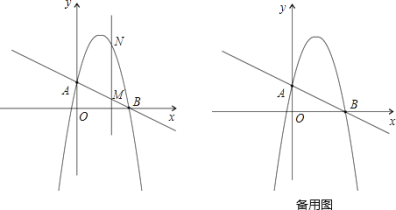
（2）设这批小龙虾放养天后的质量为（），销售单价为元/．根据以往经验可知：m与t的函数关系式为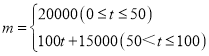，y与t的函数关系如图所示

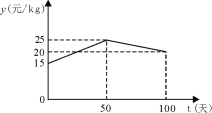
①求y与t的函数关系式；

②设将这批小龙虾放养t天后一次性出售所得利润为W元，求当为何值时，W最大？并求出W的最大值．（利润=销售总额－总成本）

Answer 1

【答案】（1）a的值为0．04，b的值为30；（2）①；②当t为55天时，w最大，最大值为180250元

【解析】

（1）由放养10天的总成本为30.4万元；放养20天的总成本为30.8万元可得答案；
（2）①分0≤t≤50、50<t≤100两种情况，结合函数图象利用待定系数法求解可得；
②就以上两种情况，根据“利润=销售总额-总成本”列出函数解析式，依据一次函数性质和二次函数性质求得最大值即可得．

解：（1）由题意，得

解得

∴的值为0．04,的值为30

(2)①当≤≤时, 设与的函数关系式为,

∵过点(0,15)和(50,25)，

∴

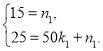
解得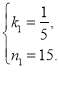

∴与的函数关系式为

当＜≤时, 设与的函数关系式为,

∵过点(50,25)和(100,20)，

∴

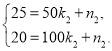
解得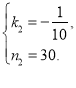

∴与的函数关系式为

∴与的函数关系式为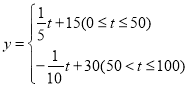

②当≤≤时,．

∵3600＞0,

∴当时,最大值=180000；

当＜≤时,

∵-10＜0,

∴当时,最大值=180250．

综上所述，当为天时,最大，最大值为180250元．