Question

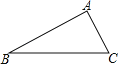
【题目】如图，在△ABC中，∠A＝90°，AB＝2，AC＝，以BC为斜边作等腰Rt△BCD，连接AD，则线段AD的长为_____．

Answer 1

【答案】

【解析】

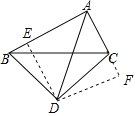
过D 作DE⊥AB于E，DF⊥AC于F，则四边形AEDF是矩形，先证明△BDE≌△CDF（AAS），可得DE＝DF，BE＝CF，以此证明四边形AEDF是正方形，可得∠DAE＝∠DAF＝45°，AE＝AF，代入AB＝2，AC＝可得BE、AE的长，再在Rt△ADE中利用特殊三角函数值即可求得线段AD的长．

过D 作DE⊥AB于E，DF⊥AC于F，

则四边形AEDF是矩形，

∴∠EDF＝90°，

∵∠BDC＝90°，

∴∠BDE＝∠CDF，

∵∠BED＝∠CFD＝90°，BD＝DC，

∴△BDE≌△CDF（AAS），

∴DE＝DF，BE＝CF，

∴四边形AEDF是正方形

∴∠DAE＝∠DAF＝45°，

∴AE＝AF，

∴2﹣BE＝+BE，

∴BE＝，

∴AE＝，

∴AD＝AE＝，

故答案为：．