��Ŀ����
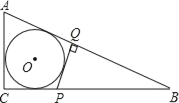
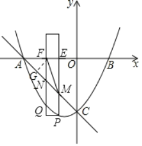
����Ŀ����ͼ��������y��![]() x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B������Ϊ��3��0������C������Ϊ��0����5������һ����Ϊ1�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F��
x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B������Ϊ��3��0������C������Ϊ��0����5������һ����Ϊ1�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F��
��1���������ߵĽ���ʽ����A�����ꣻ
��2������M��N�����߶�AC��ʱ������MF�����sin��AMF��![]() �����Q�����ꣻ
�����Q�����ꣻ
��3���ھ��ε�ƽ�ƹ����У��Ƿ�����Ե�P��Q��M��NΪ������ı�����ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��y��![]() x2+
x2+![]() x��5��A����5��0������2��Q���꣨��4����
x��5��A����5��0������2��Q���꣨��4����![]() ������3�����ڣ���M������Ϊ����2����3����2+
������3�����ڣ���M������Ϊ����2����3����2+![]() ����3��
����3��![]() ����2��
����2��![]() ����3+
����3+![]() ����
����
��������
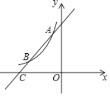
��1������B�����ꡢ��C������ֱ���뺯������ʽ���b��c��ֵ����������߽���ʽ��õ�A�����ꣻ
��2����FG��AC��G�����F���꣨m��0��������sin��AMF=![]() ���г����̼��ɽ�����⣮
���г����̼��ɽ�����⣮
��3�����ٵ�MN�ǶԽ���ʱ�����F��m��0������QN=PM���г����̼��ɽ�����⣮�ڵ�MNΪ��ʱ�����Q��m��![]() m2+
m2+![]() m-5�����P��m+1��
m-5�����P��m+1��![]() m2+
m2+![]() m-6�������������߽���ʽ���ⷽ�̼��ɣ�
m-6�������������߽���ʽ���ⷽ�̼��ɣ�
��1�����������ϵĵ�B������Ϊ��3��0������C������Ϊ��0����5��
�ཫ�����y�T![]() x2+bx+c����
x2+bx+c����![]() ��
��
���b��![]() ��c����5��
��c����5��
�������ߵĽ���ʽΪy��![]() x2+
x2+![]() x��5��
x��5��
��y=0�ɵ�x=3��-5
���A�������ǣ���5��0����
��2����FG��AC��G�����F���꣨m��0����
��AF��m+5��AE��EM��m+6��FG��![]() ��m+5����FM��
��m+5����FM��![]() ��
��
��sin��AMF��![]() ��
��
��![]() ��
��
��![]() ��
��
�����õ�2m2+19m+44��0��
�ࣨm+4����2m+11����0��
��m����4��5.5����������
���Q���꣨��4����![]() ����
����
��3���ٵ�MN�ǶԽ���ʱ����M��y����Ҳ࣬���F��m��0����
��ֱ��AC����ʽΪy����x��5��
���N��m����m��5������M��m+1����m��6����
��QN��PM��
�ੁm��5����![]() m2+
m2+![]() m��5����[
m��5����[![]() ��m+1��2+
��m+1��2+![]() ��m+1����5]������m��6����
��m+1����5]������m��6����
���m����3+![]() ��3��
��3��![]() ����������
����������
��ʱM����2+![]() ����3��
����3��![]() ����
����
��MN�ǶԽ���ʱ����N�ڵ�A�����ʱ�����F��m��0����
�ࣨ![]() m2+
m2+![]() m��5��������m��5��������m��6����[
m��5��������m��5��������m��6����[![]() ��m+1��2+
��m+1��2+![]() ��m+1����5]��
��m+1����5]��
���m����3��![]() ��3+
��3+![]() ����������
����������
��ʱM����2��![]() ����3+
����3+![]() ����
����
�ڵ�MNΪ��ʱ�����Q��m��![]() m2+
m2+![]() m��5�����P��m+1��
m��5�����P��m+1��![]() m2+
m2+![]() m��6����
m��6����
��NQ��PM��
��![]() m2+
m2+![]() m��6��
m��6��![]() ��m+1��2+
��m+1��2+![]() ��m+1����5
��m+1����5
���m����3��
���M���꣨��2����3����
�����������Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ����M������Ϊ����2����3����2+![]() ����3��
����3��![]() ����2��
����2��![]() ����3+
����3+![]() ����
����