Question

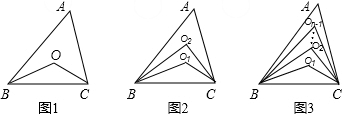
如图1，在△ABC中，∠ABC，∠ACB的角平分线交于点O，则∠BOC=90°+

1

2

∠A=

1

2

×180°+

1

2

∠A．
如图2，在△ABC中，∠ABC，∠ACB的两条三等分角线分别对应交于O₁，O₂，则∠BO₁C=

2

3

×180°+

1

3

∠A，∠BO₂C=

1

3

×180°+

2

3

∠A．
根据以上阅读理解，你能猜想（n等分时，内部有n-1个点）（用n的代数式表示）∠BO_n-1C=（　　）

• A、

  2

  n

  ×180°+

  1

  n

  ∠A
• B、

  1

  n

  ×180°+

  2

  n

  ∠A
• C、

  n

  n-1

  ×180°+

  1

  n-1

  ∠A
• D、

  1

  n

  ×180°+

  n-1

  n

  ∠A

Answer 1

分析：本题可分别将n=1，2，3…的情况列出来，分别解出∠BOC的度数，再进行总结归纳即可．

解答：解：n=1时，∠BO_n-1C=180°-∠A；
n=2时，∠BO_n-1C=180°-

1

2

（180°-∠A）=

1

2

×180°+

1

2

∠A；
n=3时，∠BO_n-1C=180°-

2

3

（180°-∠A）=

1

3

×180°+

2

3

∠A；
…
所以当n=n时，∠BO_n-1C=

1

n

×180°+

n-1

n

∠A．
故答案选D．

点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．