题目内容
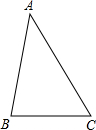 在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AB、AC交于E、D两点.
在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AB、AC交于E、D两点.(1)请用尺规作图作出AB的垂直平分线DE;
(2)连接BD,证明:△ABC∽△BDC.
考点:相似三角形的判定,作图—基本作图
专题:
分析:(1)根据线段垂直平分线的作法作出线段AB的垂直平分线即可;
(2)先根据线段垂直平分线的性质求出∠BAC=∠ABD,故可得出∠CBD的度数,再由相似三角形的判定定理即可得出结论.
(2)先根据线段垂直平分线的性质求出∠BAC=∠ABD,故可得出∠CBD的度数,再由相似三角形的判定定理即可得出结论.
解答: (1)解:如图所示;
(1)解:如图所示;
(2)证明:∵DE是线段AB的垂直平分线,
∴AD=BD.
∵∠BAC=40°,∠ABC=80°,
∴∠BAC=∠ABD,
∴∠CBD=80°-40°=40°,即∠CBD=∠BAC.
∵∠C是公共角.
∴△ABC∽△BDC.
 (1)解:如图所示;
(1)解:如图所示;(2)证明:∵DE是线段AB的垂直平分线,
∴AD=BD.
∵∠BAC=40°,∠ABC=80°,
∴∠BAC=∠ABD,
∴∠CBD=80°-40°=40°,即∠CBD=∠BAC.
∵∠C是公共角.
∴△ABC∽△BDC.
点评:本题考查的是相似三角形的判定,熟知有两组角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如果多项式x2-mx+6分解因式的结果是(x-3)(x+n),那么m,n的值分别是( )
| A、m=-2,n=5 |
| B、m=2,n=5 |
| C、m=5,n=-2 |
| D、m=-5,n=2 |

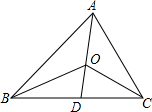 已知△ABC,三个内角的角平分线交于点O,∠OCB=30°,求∠BOD.
已知△ABC,三个内角的角平分线交于点O,∠OCB=30°,求∠BOD.