题目内容
 已知:如图,菱形ABCD的对角线AC与BD交于点O,延长BA到E,使AE=
已知:如图,菱形ABCD的对角线AC与BD交于点O,延长BA到E,使AE=| 1 |
| 2 |
延长DE交CA的延长线于F.
求证:OE=
| 1 |
| 2 |
分析:根据菱形的性质推出AB=CD,AB∥CD,AC⊥BD,根据平行线分线段成比例定理求出
=
,求出E为DF的中点,根据直角三角形斜边上 的中线性质求出即可.
| EF |
| DF |
| 1 |
| 2 |
解答: 证明:∵菱形ABCD,
证明:∵菱形ABCD,
∴AB=CD,AB∥CD,AC⊥BD,
∵AE=
AB,
∴AE=
CD,又AB∥CD,
∴△FAE∽△FCD,且相似比为1:2,
∴
=
=
,
∴E为DF的中点,
∵∠AOD=90°,
∴OE=
DF.
 证明:∵菱形ABCD,
证明:∵菱形ABCD,∴AB=CD,AB∥CD,AC⊥BD,
∵AE=
| 1 |
| 2 |
∴AE=
| 1 |
| 2 |
∴△FAE∽△FCD,且相似比为1:2,
∴
| EF |
| FD |
| AE |
| CD |
| 1 |
| 2 |
∴E为DF的中点,
∵∠AOD=90°,
∴OE=
| 1 |
| 2 |
点评:本题主要考查对菱形的性质,直角三角形斜边上的中线性质,平行线分线段成比例定理等知识点的理解和掌握,能推出E为DF的中点是解此题的关键.

练习册系列答案
相关题目
 17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
 22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.
22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.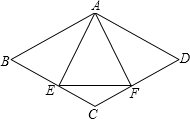 已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF; (2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.
(2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.