题目内容
如图,以边长为| 2 |
 且与直线AB只有一个公共点.
且与直线AB只有一个公共点.(1)求直线AB的解析式.
(2)求抛物线y=x2+bx+c的解析式.
分析:(1)根据正方形对角线的性质,当AB=
时,OA=OB=1,可求直线AB的解析式;
(2)把B(0,-1)代入抛物线y=x2+bx+c中得c=-1,联立直线与抛物线解析式,得方程组,消去y,得关于x的一元二次方程,当直线与抛物线有唯一公共点时,△=0,可求b;
| 2 |
(2)把B(0,-1)代入抛物线y=x2+bx+c中得c=-1,联立直线与抛物线解析式,得方程组,消去y,得关于x的一元二次方程,当直线与抛物线有唯一公共点时,△=0,可求b;
解答:解:(1)设直线AB的解析式为:y=kx+b,
由已知可得A(-1,0),B(0,-1)则
∴
.
∴直线AB的解析式为:y=-x-1.
(2)把B(0,-1)代入抛物线y=x2+bx+c中得c=-1,联立
得x2+(b+1)x=0,
当△=0时,解得b=-1.
∴抛物线解析式为:y=x2-x-1.
由已知可得A(-1,0),B(0,-1)则
|
∴
|
∴直线AB的解析式为:y=-x-1.
(2)把B(0,-1)代入抛物线y=x2+bx+c中得c=-1,联立
|
得x2+(b+1)x=0,
当△=0时,解得b=-1.
∴抛物线解析式为:y=x2-x-1.
点评:本题考查了正方形的性质,一次函数,二次函数解析式的求法;本题需要数形结合,分类讨论.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
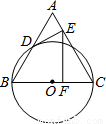
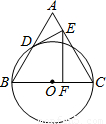
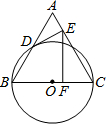 如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,则EF=
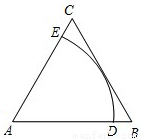
如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,则EF= 如图,以边长为6的正△ABC的顶点A为圆心,作弧DE与BC相切,分别交AB,AC于点D,E,则弧DE的长为:
如图,以边长为6的正△ABC的顶点A为圆心,作弧DE与BC相切,分别交AB,AC于点D,E,则弧DE的长为: