题目内容
（2006•玉溪）如图，以边长为6的正△ABC的顶点A为圆心，作弧DE与BC相切，分别交AB，AC于点D，E，则弧DE的长为： ．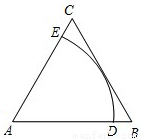
【答案】分析：圆心角∠A=60°，要求弧DE的长，通过扇形的弧长公式知，需要求出扇形的半径，可以通过勾股定理解决．
解答：
解：连接AF，
设F为BC的中点，BF=6÷2=3，
AF=
=3
，
弧DE的长=
×2π×3
=
π．
点评：本题考查了扇形的弧长公式，求扇形的弧长，关键是求出圆心角和扇形的半径．
解答：
解：连接AF，设F为BC的中点，BF=6÷2=3，
AF=
=3，弧DE的长=
×2π×3=π．点评：本题考查了扇形的弧长公式，求扇形的弧长，关键是求出圆心角和扇形的半径．
练习册系列答案
相关题目
