题目内容
如图,⊙O内切于△ABC,切点分别为D、E、F.已知∠B=50°,∠C=60°,连接DE、DF,求∠EDF.
【答案】分析:连接OE和OF,求出∠EOF即可知道∠EDF,根据三角形内角和定理得出∠A,从而得出∠EOF.即得∠EDF.
解答: 解:连接OE、OF.
解:连接OE、OF.
∵∠B=50°,∠C=60°,
∴∠A=70°;
∵AB、AC分别切⊙O于点E、F,
∴OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90,
∴∠EOF=110°,
又∵∠EDF= ∠EOF,
∠EOF,
∴∠EDF=55°.
点评:本题考查了圆周角和圆心角之间的关系和三角形内角和为180°的定理.
解答:
 解:连接OE、OF.
解:连接OE、OF.∵∠B=50°,∠C=60°,
∴∠A=70°;
∵AB、AC分别切⊙O于点E、F,
∴OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90,
∴∠EOF=110°,
又∵∠EDF=
 ∠EOF,
∠EOF,∴∠EDF=55°.
点评:本题考查了圆周角和圆心角之间的关系和三角形内角和为180°的定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
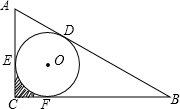 如图,⊙O内切于△ABC,切点分别为D、E、F,若∠C=90°,AD=4,BD=6,求图中阴影部分的面积.
如图,⊙O内切于△ABC,切点分别为D、E、F,若∠C=90°,AD=4,BD=6,求图中阴影部分的面积.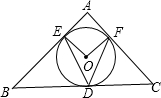
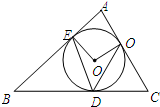 如图,⊙O内切于△ABC,切点分别为D、E、F,若∠B=40°,∠C=60°,则∠EDF的大小为
如图,⊙O内切于△ABC,切点分别为D、E、F,若∠B=40°,∠C=60°,则∠EDF的大小为 如图,⊙O内切于△ABC,切点分别为D、E、F,且DE∥BC,若AB=8cm,AD=5cm,则△ADE的周长是
如图,⊙O内切于△ABC,切点分别为D、E、F,且DE∥BC,若AB=8cm,AD=5cm,则△ADE的周长是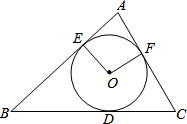 如图,⊙O内切于△ABC,切点分别为D,E,F已知∠B=60°,∠C=70°,连结OE,OF,DE,DF,那么∠EOF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F已知∠B=60°,∠C=70°,连结OE,OF,DE,DF,那么∠EOF等于( )