Question

【题目】(1)如图1，在直线上，点在、两点之间，点为线段PB的中点，点为线段的中点，若，且使关于的方程无解.

①求线段的长；

②线段的长与点在线段上的位置有关吗？请说明理由；

(2)如图2，点为线段的中点，点在线段的延长线上，试说明的值不变.

Answer 1

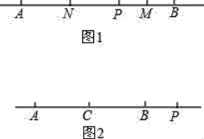
【答案】（1）①AB=4；②线段的长与点在线段上的位置无关，理由见解析；

（2）见解析.

【解析】

（1）由关于的方程无解．可得=0，从而可求得n的值；
（2）根据线段中点的定义可知PN=AP，PM=PB，从而得到MN=（PA+PB）=AB，于是可求；
（3）设AB=a，BP=b．先表示PB+PA的长，然后再表示PC的长，最后代入计算即可．

解：（1）①∵关于的方程无解．

∴=0，
解得：n=4．
故AB=4．
②线段的长与点在线段上的位置无关，理由如下：

∵M为线段PB的中点，
∴PM= PB．
同理：PN= AP．．
∴MN=PN+PM= （PB+AP）= AB= ×4=2．
∴线段MN的长与点P在线段AB上的位置无关．
（2）设AB=a，BP=b，

则PA+PB=a+b+b=a+2b．
∵C是AB的中点，

，

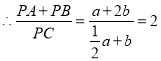所以的值不变.