题目内容

已知直线y=kx+1与x轴交于点A，与y轴交于点B，与抛物线y=ax²-x+c交于点A和点C（ $数学公式$ ， $数学公式$ ），抛物线的顶点为D．
（1）求直线和抛物线的解析式；
（2）求△ABD的面积．

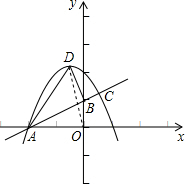解：（1）∵直线y=kx+1过点C（ $\text{[math]}$ ， $\text{[math]}$ ），
∴k= $\text{[math]}$ ，
∴y= $\text{[math]}$ x+1；
∴A（-2，0），
∵抛物线y=ax²-x+c交于点A和点C（ $\text{[math]}$ ， $\text{[math]}$ ），
∴ $\text{[math]}$
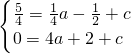
即 $\text{[math]}$ ，
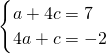解得 $\text{[math]}$ ，
∴抛物线解析式为y=-x²-x+2；

（2）可求得顶点D（- $\text{[math]}$ ， $\text{[math]}$ ），
连接OD；
∴S_△ABD=S_△AOD+S_△DBO-S_△ABO
= $\text{[math]}$ ．
分析：（1）已知直线y=kx+1经过点C，可将其坐标代入直线的解析式中，从而求得k的值，即可确定该直线的解析式；根据求得的直线解析式可得到点A的坐标，然后将A、C坐标代入抛物线的解析式中，即可求得待定系数的值，从而得到抛物线的解析式；
（2）根据（1）所得抛物线的解析式，利用公式法或配方法可求得顶点D的坐标．由于△ABD的面积无法直接求出，可连接OD，将其面积转化为△AOD、△OBD的面积和减去△ABO的面积，根据A、B、D三点的坐标，分别求出各图形的面积，即可得到△ABD的面积．
点评：此题考查了用待定系数法求函数解析式的方法以及图形面积的求法，属于基础题，需注意的是不规则图形的面积通常转化为规则图形的面积的和差来解．