题目内容
 某航空公司托运行李的费用y元与托运行李的质量x(kg)之间的函数关系如图所示.根据图中的信息,求:
某航空公司托运行李的费用y元与托运行李的质量x(kg)之间的函数关系如图所示.根据图中的信息,求:(1)y与x函数解析式;
(2)免费托运行李质量的范围.
分析:(1)分两种情况当0<x≤19时,是一个常数函数,当x>19时设y与x之间的函数关系式为y=kx+b,由函数图象由待定系数法可以直接求出函数的解析式;
(2)由题意得知免费托运,就是运费为0,当y=0代入求出函数的解析式就可以得出结论;
(2)由题意得知免费托运,就是运费为0,当y=0代入求出函数的解析式就可以得出结论;
解答:(1)当x>19时,设y与x之间的函数关系式为y=kx+b,由函数图象,得
,
解得:
,
∴y=30x-570(x>19);
当0<x≤19时,y=0;
(2)由题意,得
当y=0时,x=19,
∴免费托运行李质量的范围是不超过19千克.
|
解得:
|
∴y=30x-570(x>19);
当0<x≤19时,y=0;
(2)由题意,得
当y=0时,x=19,
∴免费托运行李质量的范围是不超过19千克.
点评:本题是一道一次函数的实际运用试题,考查了待定系数法求一次函数的解析式的运用,在解答本题时求出一次函数的解析式是关键.

练习册系列答案
相关题目
 如图,某航空公司托运行李的费用与托运行李的重量的关系为一次函数,由图可知行李的重量只要不超过
如图,某航空公司托运行李的费用与托运行李的重量的关系为一次函数,由图可知行李的重量只要不超过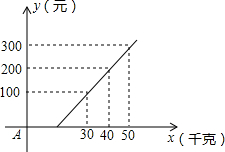 (2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( )
(2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( ) 如图,表示的是某航空公司托运行李的费用y(元)与托运行李的质量x(千克)的关系,由图中可知行李的质量,只要不超过
如图,表示的是某航空公司托运行李的费用y(元)与托运行李的质量x(千克)的关系,由图中可知行李的质量,只要不超过