Question

【题目】阅读探究问题：

（1）方法感悟：

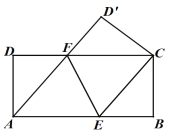
如图①，在正方形中，点分别为，边上的点，且满足，连接，求证．

感悟解题方法，并完成下列填空：

将绕点顺时针旋转90°得到，此时与重合，由旋转可得：

，

∴，

因此，点在同一条直线上，

∵，∴，

∵，∴．

即．

又

∴．

∴，故．

（2）方法迁移：

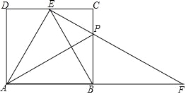
如图②，将沿斜边翻折得到，点分别为边上的点，且．试猜想之间有何数量关系，并证明你的猜想．

（3）问题拓展：

如图③，在四边形中，，分别为上的点，满足，试猜想当与满足什么关系时，可使得．请直接写出你的猜想（不必说明理由）．

Answer 1

【答案】（1），，；（2），见解析；（3）

【解析】

（1）作辅助线，构建全等三角形，证明点，，在同一条直线上，再证明，可得结论；

（2）同理作辅助线，如图②，将绕顺时针旋转的度数，此时，与重合，证明，同理可以得出；

（3）当与满足时，可使得，理由是将绕顺时针旋转的度数，同理证明，得．

解：（1）将绕点顺时针旋转得到，此时与重合，由旋转可得：

，，，，

，

因此，点，，在同一条直线上．

．

，

．

即．

又，

．

，故．

故答案：，，；

（2）如图②，，理由是：

将绕顺时针旋转的度数，此时，与重合，

由旋转得：，，，

，

同理得：点，，在同一条直线上，

，

，

，

，

，，

，

，

；

（3）当与满足时，可使得，理由是：

将绕顺时针旋转的度数，此时，与重合，

由旋转得：，，，

，

点，，在同一条直线上，

，

，

，

，

，，

，

，

；