Question

【题目】如图，在中，，以为直径的交于点，切线交于点.

（1）求证：；

（2）若，，求的长.

Answer 1

【答案】（1）见解析；（2）

【解析】

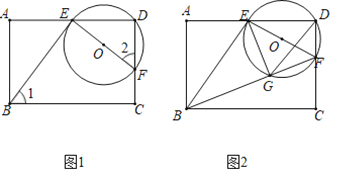
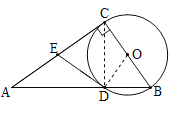
（1）连接OD．只要证明∠A+∠B=90°，∠ADE+∠B=90°即可解决问题；

（2）首先证明AC=2DE=20．在Rt△ADC中，由勾股定理得到DC的长，设BD=x．在Rt△BDC中，BC2=x2+122．在Rt△ABC中，BC2=（x+16）2﹣202，可得x2+122=（x+16）2﹣202，解方程即可解决问题．

（1）连接OD．

∵DE是切线，∴∠ODE=90°，∴∠ADE+∠BDO=90°．

∵∠ACB=90°，∴∠A+∠B=90°．

∵OD=OB，∴∠B=∠BDO，∴∠ADE=∠A．

（2）连接CD．

∵∠ADE=∠A，∴AE=DE．

∵BC是⊙O的直径，∠ACB=90°，

∴EC是⊙O的切线，∴ED=EC，∴AE=EC．

∵DE=10，∴AC=2DE=20，

在Rt△ADC中，DC12，

设BD=x．在Rt△BDC中，BC2=x2+122．

在Rt△ABC中，BC2=（x+16）2﹣202，

∴x2+122=（x+16）2﹣202，

解得x=9，∴BC15．