题目内容
 如图,在半径为2,圆心角等于90°的扇形AOB内部作一个直角梯形OBCD,使点C在
如图,在半径为2,圆心角等于90°的扇形AOB内部作一个直角梯形OBCD,使点C在 上,且为
上,且为 的中点,D在OA上,则阴影部分的面积为(结果保留π) .
的中点,D在OA上,则阴影部分的面积为(结果保留π) .
【答案】分析:连接OC,则可得∠AOC=∠BOC=45°,△ODC是等腰直角三角形,从而求出OD,根据S阴影=S扇形-S梯形OBCD即可得出答案.
解答:解:连接OC,

∵点C为 的中点,
的中点,
∴∠AOC=∠BOC=45°,
∴△ODC是等腰直角三角形,
∵OC=2,
∴OD=CD= ,
,
则S阴影=S扇形-S梯形OBCD= -
- (
( +2)×
+2)× =π-1-
=π-1- .
.
故答案为:π-1- .
.
点评:本题考查了扇形的面积计算及梯形的知识,判断出△ODC是等腰直角三角形是解答本题的关键.
解答:解:连接OC,

∵点C为
 的中点,
的中点,∴∠AOC=∠BOC=45°,
∴△ODC是等腰直角三角形,
∵OC=2,
∴OD=CD=
 ,
,则S阴影=S扇形-S梯形OBCD=
 -
- (
( +2)×
+2)× =π-1-
=π-1- .
.故答案为:π-1-
 .
.点评:本题考查了扇形的面积计算及梯形的知识,判断出△ODC是等腰直角三角形是解答本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
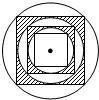 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
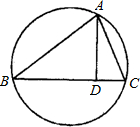 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为 8、如图:在半径为1的圆中,弦CD垂直平分AB,则CD=
8、如图:在半径为1的圆中,弦CD垂直平分AB,则CD= 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是