题目内容
如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交与点D.
 (1)判断CD与⊙O的位置关系并说明理由;
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.
解 (1) CD与⊙O的位置关系![]() 是相切,理由如下:
是相切,理由如下:
作直径CE,连结AE.
∵CE是直径, ∴∠EAC=90°,∴∠E+∠ACE=90°,
∵CA=CB,∴∠B=∠CAB,∵AB∥CD,
∴∠ACD=∠CAB,∵∠B=∠E,∠ACD=∠E,
∴∠ACE+∠ACD=90°,即∠DCO=90°,
∴OC⊥D C,∴CD与⊙O相切.
(2)∵CD∥AB,OC⊥D C,∴OC⊥A B,
又∠ACB=120°,∴∠OCA=∠OCB=60°,
∵OA=OC,∴△OAC是等边三角形,
∴∠DOA=60°,
∴在Rt△DCO中,![]() =
=![]() ,
,
∴DC=![]() OC=
OC=![]() OA=2
OA=2![]() .
.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.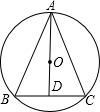 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.