题目内容
已知点A在线段CD上，△ACB与△ADE都是直角三角形，∠C=∠D=90°，△BAE是等腰直角三角形，且∠BAE=90°．求证：CD=BC+ED．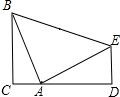
证明：∵△BAE是等腰直角三角形，
∴BA=EA，∠BAE=90°，
∴∠BAC+∠EAD=90°，
∵∠D=90°，
∴∠EAD+∠AED=90°，
∴∠BAC=∠AED，
∵在△BCA和△ADE中，
，
∴△BCA≌△ADE（AAS），
∴CB=AD，ED=AC，
∴CD=CA+AD=BC+ED．
∴BA=EA，∠BAE=90°，
∴∠BAC+∠EAD=90°，
∵∠D=90°，
∴∠EAD+∠AED=90°，
∴∠BAC=∠AED，
∵在△BCA和△ADE中，
|
∴△BCA≌△ADE（AAS），
∴CB=AD，ED=AC，
∴CD=CA+AD=BC+ED．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
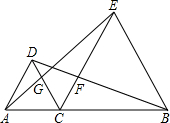如图：已知点C在线段AB上，向AB的同侧分别作等边三角形△ACD、△CBE，连接AE交CD于G，连接BD交CE于F．
已知点A在线段CD上，△ACB与△ADE都是直角三角形，∠C=∠D=90°，△BAE是等腰直角三角形，且∠BAE=90°．求证：CD=BC+ED．
已知点A在线段CD上，△ACB与△ADE都是直角三角形，∠C=∠D=90°，△BAE是等腰直角三角形，且∠BAE=90°．求证：CD=BC+ED．