题目内容
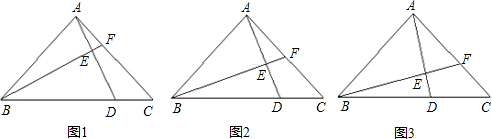
如图等腰Rt△ABC中AB=AC,D为斜边BC上的动点,若BD=nCD,BF⊥AD交AD于E、AC于F.(1)如图1,若n=3时,则
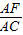 =______;
=______;(2)如图2,若n=2时,求证:
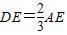 ;
;(3)当n=______
【答案】分析:(1)过C作CG⊥AC交AD的延长线与G点,由题意可证明△ABD∽△GCD, ,tan∠EAF=
,tan∠EAF= ,即可证明AF:AC=1:3;
,即可证明AF:AC=1:3;
(2)过D作DG∥BF交AC与F点,CD:DB=1:2,CG:GF=1:2,由第一问知AF:AC=CD:BD=1:2,所以,AF:FC=1:1,即可证明DE:AE=2:3;
(3)过D作DG∥BF交AC与F点,设CG=k,则:GF=nk,再由第二问的解题方法可求得n的值.
解答: 解:(1)过C作CG⊥AC交AD的延长线于G点,如图1所示:
解:(1)过C作CG⊥AC交AD的延长线于G点,如图1所示:
∵CG⊥AC,
∴CG∥AB.
∴△ABD∽△GCD.
∴ .
.
∵AB=AC,
∴ .
.
∴tan∠EAF= .
.
∴ .
.
∵在Rt△ABF中,△AEF∽△BAF,
∴ =
= =
= .
.
∴ =
= .
.

(2)过D作DG∥BF交AC于G点,如图2所示:
∵CD:DB=1:2,
∴CG:GF=1:2.
∵由第一问知AF:AC=CD:BD=1:2,
∴AF:FC=1:1.
∴AF:FG=3:2.
∴AE:ED=3:2.
∴DE= AE.
AE.
(3)过D作DG∥BF交AC于G点,如图3所示:
CD:BD=AF:AC=1:n,
CG:GF=1:n,
设CG=k,则:
GF=nk,
∵AE=2DE,
∴AF=2FG.
∴AF=2nk.
∴AC=3nk+k.
∵AC=nAF,
∴3nk+k=2n2k.
∴n= .
.
点评:本题考查了相似三角形的判定与性质.
 ,tan∠EAF=
,tan∠EAF= ,即可证明AF:AC=1:3;
,即可证明AF:AC=1:3;(2)过D作DG∥BF交AC与F点,CD:DB=1:2,CG:GF=1:2,由第一问知AF:AC=CD:BD=1:2,所以,AF:FC=1:1,即可证明DE:AE=2:3;
(3)过D作DG∥BF交AC与F点,设CG=k,则:GF=nk,再由第二问的解题方法可求得n的值.
解答:
 解:(1)过C作CG⊥AC交AD的延长线于G点,如图1所示:
解:(1)过C作CG⊥AC交AD的延长线于G点,如图1所示:∵CG⊥AC,
∴CG∥AB.
∴△ABD∽△GCD.
∴
 .
.∵AB=AC,
∴
 .
.∴tan∠EAF=
 .
.∴
 .
.∵在Rt△ABF中,△AEF∽△BAF,
∴
 =
= =
= .
.∴
 =
= .
.
(2)过D作DG∥BF交AC于G点,如图2所示:
∵CD:DB=1:2,
∴CG:GF=1:2.
∵由第一问知AF:AC=CD:BD=1:2,
∴AF:FC=1:1.
∴AF:FG=3:2.
∴AE:ED=3:2.
∴DE=
 AE.
AE.(3)过D作DG∥BF交AC于G点,如图3所示:

CD:BD=AF:AC=1:n,
CG:GF=1:n,
设CG=k,则:
GF=nk,
∵AE=2DE,
∴AF=2FG.
∴AF=2nk.
∴AC=3nk+k.
∵AC=nAF,
∴3nk+k=2n2k.
∴n=
 .
.点评:本题考查了相似三角形的判定与性质.

练习册系列答案
相关题目
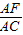 =______;
=______;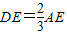 ;
;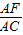 =______;
=______;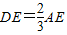 ;
;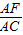 =______;
=______;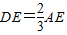 ;
;