题目内容
阅读下面计算过程:
=
=
-1;
=
=
-
;
=
=
-2;
试求:
(1)
的值为 ;
(2)
(n为正整数)的值为 .
| 1 | ||
|
1×(
| ||||
(
|
| 2 |
| 1 | ||||
|
1×(
| ||||||||
(
|
| 3 |
| 2 |
| 1 | ||
|
1×(
| ||||
(
|
| 5 |
试求:
(1)
| 1 | ||||
|
(2)
| 1 | ||||
|
考点:分母有理化
专题:阅读型
分析:(1)根据平方差公式,先找到有理化因式,再分母有理化即可;
(2)类比(1)先找到有理化因式,再分母有理化即可.
(2)类比(1)先找到有理化因式,再分母有理化即可.
解答:解:(1)原式=
=
-
;
(2)
=
-
.
故答案为
-
,
-
.
1×(
| ||||||||
(
|
=
| 7 |
| 6 |
(2)
1×(
| ||||||||
(
|
=
| n+1 |
| n |
故答案为
| 7 |
| 6 |
| n+1 |
| n |
点评:本题考查了分母有理化,解题的关键是根据平方差公式,找出有理化因式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图商店里把塑料凳整齐地叠放在一起,据图中的信息,当有12张塑料凳整齐地叠放在一起时的高度是( )
如图商店里把塑料凳整齐地叠放在一起,据图中的信息,当有12张塑料凳整齐地叠放在一起时的高度是( )| A、76cm | B、56cm |
| C、66cm | D、60cm |
 如图,AB是⊙O的直径,∠C=38°,则∠AOD等于( )
如图,AB是⊙O的直径,∠C=38°,则∠AOD等于( )| A、100° | B、102° |
| C、104° | D、10° |
当x=-
时,x3+4x2的值为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
计算:(-8)×
×0.125=( )
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
-
的绝对值是( )
| 5 |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
下列图形中,是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
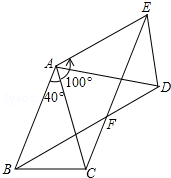 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.