题目内容
 如图,点A、C在反比例函数y=
如图,点A、C在反比例函数y=
| ||
| x |
分析:根据正三角形的性质得出OE=EB=1,设BF=m,进而表示出C点的坐标,代入解析式即可得出m的值,进而得出C点的坐标.
解答: 解:作AE⊥OB于E,CF⊥BD于F,
解:作AE⊥OB于E,CF⊥BD于F,
∵△OAB,△BCD均为正三角形,A在反比例函数y=
,
设A的横坐标是-1,
则A的纵坐标是-
,
∴OE=1,OA=2OE=2,AE=
,
∴易求OE=EB=1,设BF=m,
则C(-2-m,-
m),
代入y=
得:
m2+2m-1=0,
解得:m=-1±
,
∵m>0,
∴m=-1+
,
∴点C的坐标为:(-1-
,
-
).
 解:作AE⊥OB于E,CF⊥BD于F,
解:作AE⊥OB于E,CF⊥BD于F,∵△OAB,△BCD均为正三角形,A在反比例函数y=
| ||
| x |
设A的横坐标是-1,
则A的纵坐标是-
| 3 |
∴OE=1,OA=2OE=2,AE=
| 3 |
∴易求OE=EB=1,设BF=m,
则C(-2-m,-
| 3 |
代入y=
| ||
| x |
m2+2m-1=0,
解得:m=-1±
| 2 |
∵m>0,
∴m=-1+
| 2 |
∴点C的坐标为:(-1-
| 2 |
| 3 |
| 6 |
点评:此题主要考查了反比例函数的综合题运用正三角形的性质以及点的坐标特点,同学们应注重灵活应用综合处理函数问题这是中考中重点题型.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
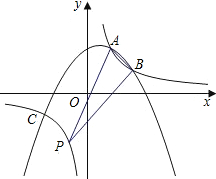 如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点.
如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点. 如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=
如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=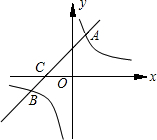 次函数y=mx+b的图象与x轴交于点C.
次函数y=mx+b的图象与x轴交于点C. 如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数
如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数