Question

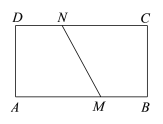
【题目】如图，一张矩形纸片ABCD，AD＝9 cm，AB＝12 cm，将纸片折叠使A，C两点重合，那么折痕MN＝________cm.

Answer 1

【答案】

【解析】

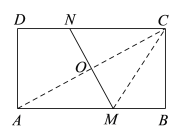
如下图，连接AC交MN于点O，连接CM，由已知易得AC=15，由折叠的性质易得AM=CM，AO=CO=，∠AOM=∠CON=90°，这样设AM=x，在Rt△BCM中建立关于x的方程即可求得CM=，进而在Rt△CMO中可求得OM=，再证△AMO≌△CNO即可得到ON=OM，由此即可得到MN=.

如下图，连接AC交MN于点O，连接CM，

∵在矩形ABCD中，BC=AD=9cm，AB=12cm，

∴AC=，

∵将矩形沿MN折叠后，点C与点A重合，

∴AM=CM，AO=CO=，∠AOM=∠CON=90°，

设AM=x，则CM=x，BM=12-x，

∵在Rt△CBM中，∠B=90°，BC=9cm，

∴，解得：，即CM=AM=，

∴在Rt△CMO中，OM=，

∵在矩形ABCD中，CD∥AB，

∴∠MAO=∠NCO，

又∵AO=CO，∠AOM=∠CON，

∴△AMO≌△CNO，

∴ON=OM，

∴MN=2OM=.

故答案为：.