Question

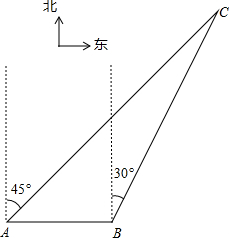（2012•攀枝花）如图，我渔政310船在南海海面上沿正东方向匀速航行，在A地观测到我渔船C在东北方向上的我国某传统渔场．若渔政310船航向不变，航行半小时后到达B处，此时观测到我渔船C在北偏东30°方向上．问渔政310船再航行多久，离我渔船C的距离最近？（假设我渔船C捕鱼时移动距离忽略不计，结果不取近似值．）

Answer 1

分析：过点C作AB的垂线，设垂足为D．由题易知∠CAB=45°，∠CBD=60°．先在Rt△BCD中，得到CD=

3

BD，再在Rt△ACD中，得到CD=AD，据此得出

BD

AB

=

3 +1

2

，然后根据匀速航行的渔船其时间之比等于路程之比，从而求出渔船行驶BD的路程所需的时间．

解答：解：作CD⊥AB交AB的延长线于点D．
∵A地观测到渔船C在东北方向上，渔船C在北偏东30°方向上，
∴∠CAB=45°，∠CBD=60°．
在Rt△BCD中，∵∠CDB=90°，∠CBD=60°，
∴CD=

3

BD．
在Rt△ACD中，∵∠CDA=90°，∠CAD=45°，
∴CD=AD，
∴

3

BD=AB+BD，
∴

BD

AB

=

1

3 -1

=

3 +1

2

，
设渔政310船再航行t分钟，离我渔船C的距离最近，
则

t

30

=

3 +1

2

，
解得t=15

3

+15．
答：渔政310船再航行（15

3

+15）分钟，离我渔船C的距离最近．

点评：本题主要考查了解直角三角形的应用-方向角问题，正确理解方向角的定义是解决本题的关键．