Question

【题目】如图1，点为直线上一点，过点作射线，使将一直角三角板的直角顶点放在点处，一边在射线上，另一边在直线的下方．

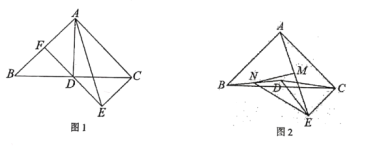
（1）将图1中的三角形板绕点按照顺时针方向旋转至图2的位置，使得落在射线上，此时旋转的角度是____°；

（2）继续将图2中的三角板绕点按顺时针方向旋转至图3的位置，使得在的内部，则_____________°；

（3）在上述直角板从图1旋转到图3的位置的过程中，若三角板绕点按每秒钟的速度旋转，当恰好为的平分线时，此时，三角板绕点运动时间为__秒，并说明理由．

Answer 1

【答案】（1）；（2）；（3）．

【解析】

(1)根据旋转的性质可知,旋转角为∠MON;

(2)如图3,利用平角的定义,结合已知条件:∠AOC:∠BOC=1：2,求得∠AOC=60°,然后由直角的性质、图中角与角的数量关系推知∠AOM-∠NOC=30°;

(3)需要分类讨论:当OM平分∠BOC时,旋转角是60°;当ON平分∠AOC时,旋转角为240°．

解:（1）根据旋转的性质可知: 旋转角为∠MON=90°, 故答案为90．

（2）如图3,

∠AOM-∠NOC=30°,理由如下: ∵∠AOC+∠BOC=180°,∠AOC:∠BOC=1:2,

∴∠AOC+2∠AOC=180°,

∴∠AOC=60°，

∴∠AON+CON=60°,①

∵∠MON=90°,

∴∠AOM+∠AON=90°,②

②-①,得∠AOM-∠CON=30°．

（3）．

理由:如图,

因点为直线上一点,

,

所以,

当恰好为的平分线时,如图所示:

,

因为旋转的角度,

所以此时三角板绕点运动的时间为,

所以当恰好的平分线时,三角板绕点的运动时间为16秒．