题目内容
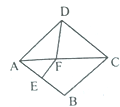
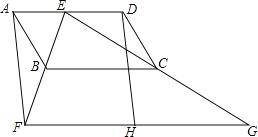
【题目】如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使
，连接EC并延长，使
，连接
为FG的中点，连接DH．
求证：四边形AFHD为平行四边形；
若
，
，
，求
的度数．
【答案】（1）证明见解析；（2）40°.
【解析】分析：（1）证明BC为△FEG的中位线，得出BC∥FG，BC=
FG，证出BC=FH，由平行四边形的性质得出AD∥BC，AD=BC，得出AD∥FH，AD=FH，即可得出结论；
（2）由平行四边形的性质得出∠DAB=∠DCB，由等腰三角形的性质得出∠BEC=∠EBC=75°，由三角形内角和定理求出∠BCE，得出∠DCB=∠DCE+∠BCE=40°，即可得出结果．
详解：
证明：
，
，
为
的中位线，
，
，
又
是FG的中点，
，
．
又
四边形ABCD是平行四边形，
，
，
，
，
四边形AFHD是平行四边形；
解：四边形ABCD是平行四边形，
，
，
，
，
，
．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
相关题目
