题目内容
10.求证:顺次连接菱形四边中点所得的四边形是矩形.分析 先写出已知和求证,如图,再进行证明,连结AC、BD,先证明EH为△ABD的中位线,则根据三角形中位线性质得到EH∥BD,同理可得FG∥BD,EF∥AC,HG∥AC,于是可判断四边形EFGH为平行四边形,接着根据菱形的性质得到AC⊥BD,则可得到EF⊥EH,然后根据矩形的判定方法得到四边形EFGH为矩形.
解答 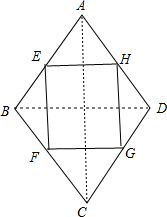 已知:点E、F、G、H为菱形ABCD各边的中点,如图,
已知:点E、F、G、H为菱形ABCD各边的中点,如图,
求证:四边形EFGH为矩形.
证明:连结AC、BD,如图,
∵点E为AB的中点,H为AD的中点,
∴EH为△ABD的中位线,
∴EH∥BD,
同理可得FG∥BD,EF∥AC,HG∥AC,
∴EH∥FG,EF∥HG,
∴四边形EFGH为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
而EH∥BD,EF∥AC,
∴EF⊥EH,
∴∠HEF=90°,
∴四边形EFGH为矩形.
点评 本题考查了中点四边形:利用三角形的中位线性质解决有关中点四边形的问题.也考查了菱形的性质和矩形的判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )
关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )
 关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )
关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )| A. | x<-3 | B. | x≤-3 | C. | x<-1 | D. | x≤-1 |
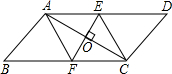 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形. 如图,在6×6的正方形网格中,每个小正方形的面积都等于1,以格点为顶点,画一个面积为13的三角形.
如图,在6×6的正方形网格中,每个小正方形的面积都等于1,以格点为顶点,画一个面积为13的三角形.
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,则不等式kx+b-$\frac{m}{x}$<0的解集为-4<x<0或x>2.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,则不等式kx+b-$\frac{m}{x}$<0的解集为-4<x<0或x>2.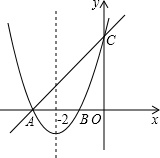 已知:如图,抛物线y1=a(x-h) 2+k与直线y2=k′x+b分别交于x轴和y轴上的点A(-3,0)和点C(0,3),已知抛物线的对称轴为直线x=-2.
已知:如图,抛物线y1=a(x-h) 2+k与直线y2=k′x+b分别交于x轴和y轴上的点A(-3,0)和点C(0,3),已知抛物线的对称轴为直线x=-2.