题目内容
 如图,?ABCD的周长为16cm,AC与BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为
如图,?ABCD的周长为16cm,AC与BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为
- A.4 cm
- B.6 cm
- C.8 cm
- D.10 cm
C
分析:由?ABCD的周长为16cm,即可求得AD+CD=8cm,又由OE⊥AC,可得DE是线段AC的垂直平分线,即可得AE=EC,继而可得△DCE的周长等于AD+CD的长.
解答:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OA=OC,
∵?ABCD的周长为16cm,
∴AD+CD=8cm,
∵OA=OC,OE⊥AC,
∴EC=AE,
∴△DCE的周长为:DE+EC+CD=DE+AE+CD=AD+CD=8(cm).
故选C.
点评:此题考查了平行四边形的性质与线段垂直平分线的性质.此题难度不大,注意数形结合思想与转化思想的应用.
分析:由?ABCD的周长为16cm,即可求得AD+CD=8cm,又由OE⊥AC,可得DE是线段AC的垂直平分线,即可得AE=EC,继而可得△DCE的周长等于AD+CD的长.
解答:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OA=OC,
∵?ABCD的周长为16cm,
∴AD+CD=8cm,
∵OA=OC,OE⊥AC,
∴EC=AE,
∴△DCE的周长为:DE+EC+CD=DE+AE+CD=AD+CD=8(cm).
故选C.
点评:此题考查了平行四边形的性质与线段垂直平分线的性质.此题难度不大,注意数形结合思想与转化思想的应用.

练习册系列答案
相关题目
 如图,将边长为a的正方形ABCD沿直线l按顺时针方向翻滚,当正方形翻滚一周时,正方形的中心O所经过的路径长为
如图,将边长为a的正方形ABCD沿直线l按顺时针方向翻滚,当正方形翻滚一周时,正方形的中心O所经过的路径长为 如图,⊙O的半径为1,正方形ABCD的边长为6,若将⊙O绕正方形ABCD滚动一周,在滚动过程中保持与正方形的边相切,则这一过程中圆心O运动的路线长为
如图,⊙O的半径为1,正方形ABCD的边长为6,若将⊙O绕正方形ABCD滚动一周,在滚动过程中保持与正方形的边相切,则这一过程中圆心O运动的路线长为 如图所示,?ABCD的对角线AC,BD相交于点O,△AOB的周长比△BOC的周长大10cm,AD=8cm,则DC=
如图所示,?ABCD的对角线AC,BD相交于点O,△AOB的周长比△BOC的周长大10cm,AD=8cm,则DC=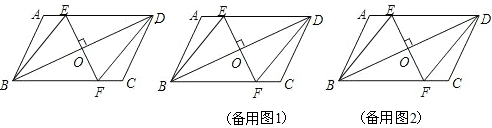
 如图,边长为a的正方形ABCD的四边贴着直线l向右无滑动“滚动”,当正方形“滚动”一周时,该正方形的中心O经过的路程是多少?顶点A经过的路程又是多少?
如图,边长为a的正方形ABCD的四边贴着直线l向右无滑动“滚动”,当正方形“滚动”一周时,该正方形的中心O经过的路程是多少?顶点A经过的路程又是多少?