题目内容
已知DE∥AC、DF∥AB,添加下列条件后,不能判断四边形DEAF为菱形的是( )
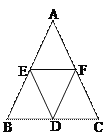
A. AD平分∠BAC
B. AB=AC且BD=CD
C. AD为中线
D. EF⊥AD
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
题目内容
已知DE∥AC、DF∥AB,添加下列条件后,不能判断四边形DEAF为菱形的是( )

A. AD平分∠BAC
B. AB=AC且BD=CD
C. AD为中线
D. EF⊥AD
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案