题目内容
(1)在下面的横线上填“>”“<”或“=”.
∵ -
- =
= ,
, -
- =
= ,
,
∴ -
- =______
=______ -
- .
.
∵ -
- =
=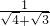 ,
, -
- =
= ,
,
∴ -
- ______
______ -
- .
.
∵ -
- =
= ,
, -
- =
=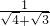 ,
,
∴ -
- ______
______ -
- .
.
(2)请你猜想 -
- 与
与 -
-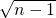 (n大于1的整数)的大小关系,并加以证明.
(n大于1的整数)的大小关系,并加以证明.
解:(1) -
- <
< -
- ,
,
 -
- <
< -
- ,
,
 -
- <
< -
- ;
;
(2)由第(1)题的结果可猜想对任意自然数n(n>1的整数)都有 -
- <
< -
-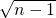 .
.
证明如下:∵ -
- =
=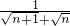 ,
, -
-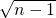 =
= ,
,
又∵n为大于1的整数,
∴n+1>n-1,∴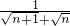 <
< ,
,
∴ -
- <
< -
-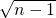 .
.
分析:分析:(1)利用公式的基本性质将 -
- 与
与 -
- 这两个数进行变形,使其分子相同,再比较它们的分母,分母大的反而小.同理可得其他式子的大小.如:
这两个数进行变形,使其分子相同,再比较它们的分母,分母大的反而小.同理可得其他式子的大小.如: -
- =
= ,
, -
- =
= ,∴
,∴ -
- <
< -
- ,同理可得其他式子全部填<.
,同理可得其他式子全部填<.
(2)由第(1)题的结果可猜对任意自然数n(n>1的整数)的结果.
点评:此题需熟练掌握 -
- =
= ,
, -
- =
= …,以及比较两个分数(式)的方法:分子相同的两个分数(式),分母大的反而小.
…,以及比较两个分数(式)的方法:分子相同的两个分数(式),分母大的反而小.
 -
- <
< -
- ,
, -
- <
< -
- ,
, -
- <
< -
- ;
;(2)由第(1)题的结果可猜想对任意自然数n(n>1的整数)都有
 -
- <
< -
-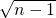 .
.证明如下:∵
 -
- =
=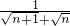 ,
, -
-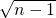 =
= ,
,又∵n为大于1的整数,
∴n+1>n-1,∴
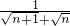 <
< ,
,∴
 -
- <
< -
-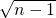 .
.分析:分析:(1)利用公式的基本性质将
 -
- 与
与 -
- 这两个数进行变形,使其分子相同,再比较它们的分母,分母大的反而小.同理可得其他式子的大小.如:
这两个数进行变形,使其分子相同,再比较它们的分母,分母大的反而小.同理可得其他式子的大小.如: -
- =
= ,
, -
- =
= ,∴
,∴ -
- <
< -
- ,同理可得其他式子全部填<.
,同理可得其他式子全部填<.(2)由第(1)题的结果可猜对任意自然数n(n>1的整数)的结果.
点评:此题需熟练掌握
 -
- =
= ,
, -
- =
= …,以及比较两个分数(式)的方法:分子相同的两个分数(式),分母大的反而小.
…,以及比较两个分数(式)的方法:分子相同的两个分数(式),分母大的反而小. 
练习册系列答案
相关题目


 13、
13、 (Ⅰ)已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.
(Ⅰ)已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.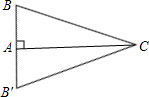 要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长.
要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长. 21、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段EF与图中哪一条线段相等?先将你的猜想出的结论填写在下面的横线上,然后再加以证明.
21、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段EF与图中哪一条线段相等?先将你的猜想出的结论填写在下面的横线上,然后再加以证明.