题目内容
13.已知方程$\frac{{x}^{2}+1}{2x}$-$\frac{x}{{x}^{2}+1}$=3,如果设$\frac{x}{{x}^{2}+1}$=y,那么原方程可化为关于y的整式方程,它可以是2y2+6y-1=0.分析 用y代替方程中的$\frac{x}{{x}^{2}+1}$得到$\frac{1}{2y}$-y=3,然后把方程化为整式方程即可.
解答 解:设$\frac{x}{{x}^{2}+1}$=y,
原方程可化为$\frac{1}{2y}$-y=3,
化为整式方程为2y2+6y-1=0.
故答案为2y2+6y-1=0.
点评 本题考查了换元法解分式方程:解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法.换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理.

练习册系列答案
相关题目
4.某超市在“元旦”促销期间规定:超市内所有商品按标价的80%出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额=商品的折扣+相应的奖券金额,例如:购买标价为440元的商品,则消费金额为:440+80%=352元,获得的优惠额为:440×(1-80%)+40=128元.
(1)若购买一件标价为880元的商品,则消费金额为640元,获得的优惠额是290元.
(2)若购买一件商品的消费金额a在100≤a≤600之间,请用含a的代数式表示优惠额;
(3)①某顾客购买一件商品的消费金额在100元与800元之间(含100元,不含800元),她能否获得230元的优惠额?若能,求出该商品的标价;若不能请说明理由.
②某顾客购买一件商品时,她能否获得260元的优惠额?请说明理由.
| 消费金额a(元)的范围 | 100≤a≤400 | 400≤a≤600 | 600≤a≤800 |
| 获得奖券金额(元) | 40 | 100 | 130 |
(1)若购买一件标价为880元的商品,则消费金额为640元,获得的优惠额是290元.
(2)若购买一件商品的消费金额a在100≤a≤600之间,请用含a的代数式表示优惠额;
(3)①某顾客购买一件商品的消费金额在100元与800元之间(含100元,不含800元),她能否获得230元的优惠额?若能,求出该商品的标价;若不能请说明理由.
②某顾客购买一件商品时,她能否获得260元的优惠额?请说明理由.
8.如果a<b<0,那么下列结论一定成立的是( )
| A. | 2a>3a | B. | a-b>0 | C. | ab<b2 | D. | a2<b2 |
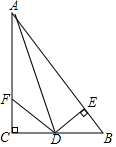 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.