题目内容
已知:抛物线y= (x-1)2-3.
(x-1)2-3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
解:(1)抛物线y= (x-1)2-3,
(x-1)2-3,
∵a= >0,
>0,
∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a= >0,
>0,
∴函数y有最小值,最小值为-3;
(3)令x=0,则y= (0-1)2-3=-
(0-1)2-3=- ,
,
所以,点P的坐标为(0,- ),
),
令y=0,则 (x-1)2-3=0,
(x-1)2-3=0,
解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0),
当点P(0,- ),Q(-1,0)时,设直线PQ的解析式为y=kx+b,
),Q(-1,0)时,设直线PQ的解析式为y=kx+b,
则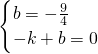 ,
,
解得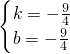 ,
,
所以直线PQ的解析式为y=- x-
x- ,
,
当P(0,- ),Q(3,0)时,设直线PQ的解析式为y=mx+n,
),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则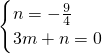 ,
,
解得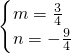 ,
,
所以,直线PQ的解析式为y= x-
x- ,
,
综上所述,直线PQ的解析式为y=- x-
x- 或y=
或y= x-
x- .
.
分析:(1)根据二次函数的性质,写出开口方向与对称轴即可;
(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;
(3)分别求出点P、Q的坐标,再根据待定系数法求函数解析式解答.
点评:本题主要考查了二次函数的性质,二次函数的最值问题,待定系数法求函数解析式,以及抛物线与x轴的交点问题,是基础题,熟记二次函数的开口方向,对称轴解析式与二次函数的系数的关系是解题的关键.
 (x-1)2-3,
(x-1)2-3,∵a=
 >0,
>0,∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a=
 >0,
>0,∴函数y有最小值,最小值为-3;
(3)令x=0,则y=
 (0-1)2-3=-
(0-1)2-3=- ,
,所以,点P的坐标为(0,-
 ),
),令y=0,则
 (x-1)2-3=0,
(x-1)2-3=0,解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0),
当点P(0,-
 ),Q(-1,0)时,设直线PQ的解析式为y=kx+b,
),Q(-1,0)时,设直线PQ的解析式为y=kx+b,则
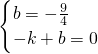 ,
,解得
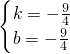 ,
,所以直线PQ的解析式为y=-
 x-
x- ,
,当P(0,-
 ),Q(3,0)时,设直线PQ的解析式为y=mx+n,
),Q(3,0)时,设直线PQ的解析式为y=mx+n,则
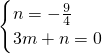 ,
,解得
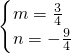 ,
,所以,直线PQ的解析式为y=
 x-
x- ,
,综上所述,直线PQ的解析式为y=-
 x-
x- 或y=
或y= x-
x- .
.分析:(1)根据二次函数的性质,写出开口方向与对称轴即可;
(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;
(3)分别求出点P、Q的坐标,再根据待定系数法求函数解析式解答.
点评:本题主要考查了二次函数的性质,二次函数的最值问题,待定系数法求函数解析式,以及抛物线与x轴的交点问题,是基础题,熟记二次函数的开口方向,对称轴解析式与二次函数的系数的关系是解题的关键.

练习册系列答案
相关题目
已知:抛物线y=x2-6x+c的最小值为1,那么c的值是( )
| A、10 | B、9 | C、8 | D、7 |