题目内容
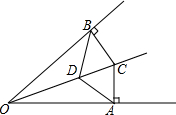 C是∠AOB角平分线上的一点,CA⊥OA,CB⊥OB(A,B为垂足),D是OC上任意一点,求证:AD=BD.
C是∠AOB角平分线上的一点,CA⊥OA,CB⊥OB(A,B为垂足),D是OC上任意一点,求证:AD=BD.考点:角平分线的性质
专题:证明题
分析:根据角平分线上的点到角的两边距离相等可得AC=BC,然后利用“HL”证明Rt△AOC和Rt△BOC全等,根据全等三角形对应角相等可得∠OCA=∠OCB,再利用“边角边”证明△ACD和△BCD全等,根据全等三角形对应边相等证明即可.
解答:解:∵C是∠AOB角平分线上的一点,CA⊥OA,CB⊥OB,
∴AC=BC,
在Rt△AOC和Rt△BOC中,
,
∴Rt△AOC≌Rt△BOC(HL),
∴∠OCA=∠OCB,
在△ACD和△BCD中,
,
∴△ACD≌△BCD(SAS),
∴AD=BD.
∴AC=BC,
在Rt△AOC和Rt△BOC中,
|
∴Rt△AOC≌Rt△BOC(HL),
∴∠OCA=∠OCB,
在△ACD和△BCD中,
|
∴△ACD≌△BCD(SAS),
∴AD=BD.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并确定出全等三角形是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
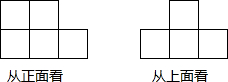 如图所示的是由小立方体搭成的几何体从正面,上面看得到的平面图形,回答下列问题:
如图所示的是由小立方体搭成的几何体从正面,上面看得到的平面图形,回答下列问题: