题目内容
二次函数y=ax2+bx+c(a≠0)中的x与y的部分对应值如下表:
| x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;
(2)当
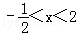 时,y<0;
时,y<0;(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是( )
A.1个 B.2个 C. 3个 D.0个
B.
解析试题分析:由表格数据可知,二次函数的对称轴为直线x=1,
所以,当x=1时,二次函数y=ax2+bx+c有最小值,最小值为-4;故(1)小题错误;
根据表格数据,当-1<x<3时,y<0,
所以, <x<2时,y<0正确,故(2)小题正确;
<x<2时,y<0正确,故(2)小题正确;
二次函数y=ax2+bx+c的图象与x轴有两个交点,分别为(-1,0)(3,0),它们分别在y轴两侧,故(3)小题正确;
综上所述,结论正确的是(2)(3)共2个.
故选B.
考点:1.二次函数的最值;2.抛物线与x轴的交点.

练习册系列答案
相关题目
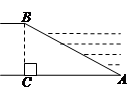
如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度 与时间
与时间 的函数关系的图象可能是( )
的函数关系的图象可能是( )

① ② ③ ④
| A.① | B.③ | C.①或③ | D.②或④ |
已知二次函数 ,下列自变量取值范围中y随x增大而增大的是( ).
,下列自变量取值范围中y随x增大而增大的是( ).
| A.x<2 | B.x<-1 | C. | D.x>-1 |
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为( )
| A.1 | B.2 | C.3 | D.4 |
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
| A.二次函数图像与x轴交点有两个 |
| B.x≥2时y随x的增大而增大 |
| C.二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间 |
| D.对称轴为直线x=1.5 |
 ),B(
),B( ),C(
),C( )为二次函数y=x²+4x-5 的图象上的三点,则
)为二次函数y=x²+4x-5 的图象上的三点,则

 的大小关系是( )
的大小关系是( ) 




 B.
B. C.
C. D.
D.
 ,则x=1或x=3;(3)若函数
,则x=1或x=3;(3)若函数 是关于x的反比例函数,则
是关于x的反比例函数,则 ;(4)已知二次函数
;(4)已知二次函数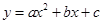 ,且a>0,a-b+c<0,则
,且a>0,a-b+c<0,则 。其中,正确的命题有( )个.
。其中,正确的命题有( )个. 的图象与x轴有两个交点,坐标分别为(
的图象与x轴有两个交点,坐标分别为( ,0),(
,0),( ,0),且
,0),且 ,图象上有一点M(
,图象上有一点M( )在x轴下方,则下列判断中正确的是( ).
)在x轴下方,则下列判断中正确的是( ).


