题目内容
等腰△ABC中，AB=AC=6cm，∠A=150°，则△ABC的面积为（ ）
| A、9cm2 |
| B、18cm2 |
| C、6cm2 |
| D、36cm2 |
考点：等腰三角形的性质,含30度角的直角三角形
专题：
分析：利用等腰三角形的性质以及外角的性质进而得出∠DAC=30°，求出CD，进而得出答案．
解答：：
解：过点C作CD⊥BA于点D，
∵∠A=150°，AB=AC=6cm，
∴∠DAC=30°，
∴DC=
AC=3cm，
∴△ABC的面积为：
×DC×AB=
×3×6=9（cm2）
故选A．
解：过点C作CD⊥BA于点D，∵∠A=150°，AB=AC=6cm，
∴∠DAC=30°，
∴DC=
| 1 |
| 2 |
∴△ABC的面积为：
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：此题主要考查了等腰三角形的性质以及三角形面积求法，得出DC的长是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
A、B两码头相距30千米，河流的水流速度为n千米/时，一条轮船的静水速度为m千米/时（m＞n），则此轮船往返A、B两码头共用（ ）小时．
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
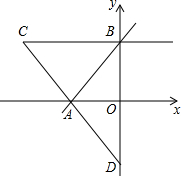如图，在平面直角坐标系中，直线y=
如图，直线a的与坐标轴围成的三形的面积是