Question

如图，在梯形ABCD中，AB∥CD，∠BCD=90°，AB=25cm，BC=24cm．将该梯形折叠，点A恰好与点D重合，BE为折痕，那么tanA=________．

Answer 1

分析：根据折叠的性质，得∠BDE=∠A，BD=AB，∠ABE=∠DBE．再由勾股定理得CD，过点D作DG⊥AB，由勾股定理得出AD、BE，从而得出答案．
解答：解：该梯形折叠，点A恰好与点D重合，BE为折痕，
∴BD=AB=25cm，
∴CD=7cm，
过点D作DG⊥AB，则CD=BG=7cm，
AG=AB-BG=18cm，
在Rt△ADG中，由勾股定理得，AD=30cm，
∴AE=15cm，
在Rt△ABE中，由勾股定理得，BE=20cm，
∴tanA===．
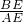故答案为：．
点评：本题考查了锐角三角函数的定义、折叠问题以及梯形的性质，是一道综合题，是中档题．