题目内容
如图，在△ABC和△CDE中，∠B =∠D=90°，C为线段BD上一点，且AC⊥CE．AB=3，DE=2，BC=6．求CD的长．
1．
【解析】
试题分析：求出∠B=∠D，∠A=∠ECD，证△ABC∽△CDE，根据相似三角形的性质得出即可．
试题解析：∵ 在△ABC中，∠B =90º，∴ ∠A +∠ACB = 90º，∵ AC⊥CE，∴ ∠ACB +∠ECD =90º，∴ ∠A=∠ECD，∵ 在△ABC和△CDE中，∵∠A=∠ECD，∠B=∠D=90º，∴ △ABC∽△CDE，∴ 
，∵ AB = 3，DE =2，BC =6，∴ CD =1．
考点：相似三角形的判定与性质．
练习册系列答案
相关题目
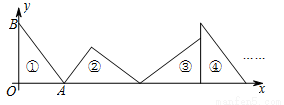
，0），B（0，4），则点B4的坐标为 ，点B2014的坐标为 ．
?
，AC＝3，则CD的长为（ ）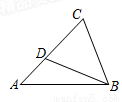
C．2 D．
，
在线段
上，且
，
，
是线段
的中点，则线段
为 
．
的三个顶点的坐标分别为
、
、
.
关于
轴对称点的坐标；（2分）
逆时针旋转
，画出图形，直接写出点
对应点的坐标；（3分）
为顶点的平行四边形的第四个顶点
的坐标．（3分）