题目内容
 (2013•武汉模拟)已知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒.
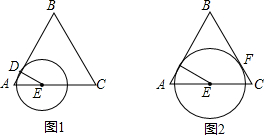
(2013•武汉模拟)已知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒.(l)如图l,判断⊙E与AB的位置关系,并证明你的结论;
(2)如图2,当⊙E与BC切于点F时,求t的值;
(3)以点C为圆心,CE长为半径作⊙C,⊙C与射线AC交于点G.当⊙C与⊙E相切时,直接写出t的值为
32±8
| ||
| 13 |
32±8
| ||
| 13 |
分析:(1)首先过点D作DM⊥AC于点M,由△ABC为等边三角形,可得∠A=60°,可得AM=
t,DM=
t,继而求得AE与ME的长,则可得在△ADE中,AD2=t2,AE2=4t2,DE2=3t2,证得AD2+DE2=AE2,继而证得AB与⊙D相切;
(2)首先连接BE、EF,由切线长定理可得BE平分∠ABC,然后由等腰三角形的性质,求得AE的长,继而求得答案;
(3)当⊙C与⊙E相切时,DE=EG=2EC,分别从当E在线段AC上时,AC=AE+EC,与当点E在AC的延长线上时,AC=AE-EC,去分析求解即可求得答案.
| 1 |
| 2 |
| ||
| 2 |
(2)首先连接BE、EF,由切线长定理可得BE平分∠ABC,然后由等腰三角形的性质,求得AE的长,继而求得答案;
(3)当⊙C与⊙E相切时,DE=EG=2EC,分别从当E在线段AC上时,AC=AE+EC,与当点E在AC的延长线上时,AC=AE-EC,去分析求解即可求得答案.
解答: 解:(1)AB与⊙E相切,…(1分)
解:(1)AB与⊙E相切,…(1分)
理由如下:过点D作DM⊥AC于点M,
∵△ABC为等边三角形,
∴∠A=60°,
在Rt△ADM中,
∵AD=t,∠A=60°,
∴AM=
t,DM=
t,
∵AE=2t,
∴ME=
t,
在Rt△DME中,DE2=DM2+EM2=3t2,
在△ADE中,∵AD2=t2,AE2=4t2,DE2=3t2,
∴AD2+DE2=AE2,
∴∠ADE=90°,
∴AB与⊙D相切; …(4分)
(2)连接BE、EF,
∵BD、BF与⊙O相切,
∴BE平分∠ABC,
∵AB=BC,
∴AE=CE,
∵AC=4,
∴AE=2,
∴t=1; …(8分)
 (3)t=
(3)t=
;
当⊙C与⊙E相切时,DE=EG=2EC,
∵DE=
t,
∴EC=
t,
有两种情形:
第一,当E在线段AC上时,AC=AE+EC,
∴2t+
t=4,
∴t=
,…(9分)
第二,当点E在AC的延长线上时,AC=AE-EC,
∴2t-
t=4,
∴t=
.(10分)
故答案为:
.
 解:(1)AB与⊙E相切,…(1分)
解:(1)AB与⊙E相切,…(1分)理由如下:过点D作DM⊥AC于点M,
∵△ABC为等边三角形,
∴∠A=60°,
在Rt△ADM中,
∵AD=t,∠A=60°,
∴AM=
| 1 |
| 2 |
| ||
| 2 |
∵AE=2t,
∴ME=
| 3 |
| 2 |
在Rt△DME中,DE2=DM2+EM2=3t2,
在△ADE中,∵AD2=t2,AE2=4t2,DE2=3t2,
∴AD2+DE2=AE2,
∴∠ADE=90°,
∴AB与⊙D相切; …(4分)
(2)连接BE、EF,
∵BD、BF与⊙O相切,
∴BE平分∠ABC,
∵AB=BC,
∴AE=CE,
∵AC=4,
∴AE=2,
∴t=1; …(8分)
 (3)t=
(3)t=32±8
| ||
| 13 |
当⊙C与⊙E相切时,DE=EG=2EC,
∵DE=
| 3 |
∴EC=
| ||
| 2 |
有两种情形:
第一,当E在线段AC上时,AC=AE+EC,
∴2t+
| ||
| 2 |
∴t=
32-8
| ||
| 13 |
第二,当点E在AC的延长线上时,AC=AE-EC,
∴2t-
| ||
| 2 |
∴t=
32+8
| ||
| 13 |
故答案为:
32±8
| ||
| 13 |
点评:此题考查了切线的性质与判定、勾股定理以及逆定理、圆与圆的位置关系以及切线长定理.此题难度较大,注意掌握辅助线的作法,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•武汉模拟)如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边交于点F;若BE:EC=m:n,则AF:FB=
(2013•武汉模拟)如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边交于点F;若BE:EC=m:n,则AF:FB= (2013•武汉模拟)如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,则圆周角∠ADC=
(2013•武汉模拟)如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,则圆周角∠ADC=