��Ŀ����
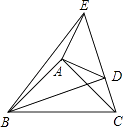
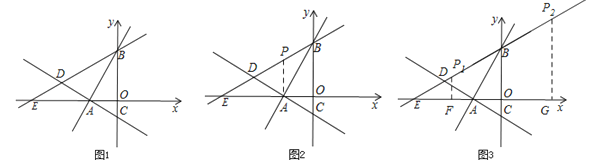
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����A��![]() ��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���
��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���![]() ����������
����������
��1�����߶�BC�ij��ȣ�
��2�����ʣ�ֱ��AC��ֱ��AB�Ƿ�ֱ����˵�����ɣ�
��3������D��ֱ��AC�ϣ���DB=DC�����D�����ꣻ
��4���ڣ�3���������£�ֱ��BD���Ƿ���ڵ�P��ʹ��A��B��P����Ϊ������������ǵ��������Σ������ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��4����2����ֱ����3��D��![]() ��1������4��P��
��1������4��P��![]() ��0������
��0������![]() ��2��������3��
��2��������3��![]() ������3��
������3��![]() ����
����
��������
�����������1����![]() ����x=3��x=��1����B��0��3����C��0����1������BC=4��
����x=3��x=��1����B��0��3����C��0����1������BC=4��
��2����A��![]() ��0����B��0��3����C��0����1������OA=
��0����B��0��3����C��0����1������OA=![]() ��OB=3��OC=1����
��OB=3��OC=1����![]() =OBOC������AOC=��BOA=90�㣬����AOC�ס�BOA������CAO=��ABO������CAO+��BAO=��ABO+��BAO=90�㣬����BAC=90�㣬��AC��AB��
=OBOC������AOC=��BOA=90�㣬����AOC�ס�BOA������CAO=��ABO������CAO+��BAO=��ABO+��BAO=90�㣬����BAC=90�㣬��AC��AB��
��3����ֱ��AC�Ľ���ʽΪy=kx+b����A��![]() ��0����C��0����1������y=kx+b����
��0����C��0����1������y=kx+b����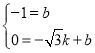 ����ã�
����ã�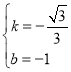 ����ֱ��AC�Ľ���ʽΪ��
����ֱ��AC�Ľ���ʽΪ��![]() ����DB=DC������D���߶�BC�Ĵ�ֱƽ�����ϣ���D��������Ϊ1������y=1����
����DB=DC������D���߶�BC�Ĵ�ֱƽ�����ϣ���D��������Ϊ1������y=1����![]() ����x=
����x=![]() ����D��������
����D��������![]() ��1����
��1����
��4����ֱ��BD�Ľ���ʽΪ��y=mx+n��ֱ��BD��x�ύ�ڵ�E����B��0��3����D��![]() ��1������y=mx+n����
��1������y=mx+n����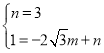 �������
�������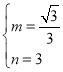 ����ֱ��BD�Ľ���ʽΪ��
����ֱ��BD�Ľ���ʽΪ��![]() ����y=0����
����y=0����![]() ����x=
����x=![]() ����E��
����E��![]() ��0������OE=
��0������OE=![]() ����tan��BEC=
����tan��BEC=![]() =
=![]() ������BEO=30�㣬ͬ������ã���ABO=30�㣬����ABE=30����
������BEO=30�㣬ͬ������ã���ABO=30�㣬����ABE=30����
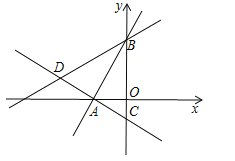
��PA=ABʱ����ͼ1����ʱ����BEA=��ABE=30�㣬��EA=AB����P��E�غϣ���P������Ϊ��![]() ��0������PA=PBʱ����ͼ2����ʱ����PAB=��PBA=30�㣬����ABE=��ABO=30�㣬����PAB=��ABO����PA��BC������PAO=90�㣬����P�ĺ�����Ϊ
��0������PA=PBʱ����ͼ2����ʱ����PAB=��PBA=30�㣬����ABE=��ABO=30�㣬����PAB=��ABO����PA��BC������PAO=90�㣬����P�ĺ�����Ϊ![]() ����x=
����x=![]() ����
����![]() ����y=2����P��
����y=2����P��![]() ��2����
��2����
��PB=ABʱ����ͼ3�����ɹ��ɶ�������ã�AB=![]() ��EB=6������P��y�����ʱ���Ǵ�ʱ��PΪP1������P1��P1F��x���ڵ�F����P1B=AB=
��EB=6������P��y�����ʱ���Ǵ�ʱ��PΪP1������P1��P1F��x���ڵ�F����P1B=AB=![]() ����EP1=6��
����EP1=6��![]() ����sin��BEO=
����sin��BEO=![]() ����FP1=
����FP1=![]() ����y=
����y=![]() ����
����![]() ����x=��3����P1����3��
����x=��3����P1����3��![]() ��������P��y����Ҳ�ʱ���Ǵ�ʱ��PΪP2������P2��P2G��x���ڵ�G����P2B=AB=
��������P��y����Ҳ�ʱ���Ǵ�ʱ��PΪP2������P2��P2G��x���ڵ�G����P2B=AB=![]() ����EP2=6+
����EP2=6+![]() ����sin��BEO=
����sin��BEO=![]() ����GP2=
����GP2=![]() ����y=
����y=![]() ����
����![]() ����x=3����P2��3��
����x=3����P2��3��![]() ����
����
������������A��B��P����Ϊ������������ǵ���������ʱ����P������Ϊ��![]() ��0������
��0������![]() ��2��������3��
��2��������3��![]() ������3��
������3��![]() ����
����

����Ŀ��ij��ѧΪ����ѧ������Զ���п�����������ȡ������ijɼ����ڶ���һ���º�ѧУ�Ծ��꼶һ���45��ѧ�����в��ԣ��ɼ����±���
��Զ�ɼ���cm�� | 160 | 170 | 180 | 190 | 200 | 220 |
���� | 3 | 9 | 6 | 9 | 15 | 3 |
��Щ�˶�Ա��Զ�ɼ�����λ���������ֱ��ǣ� ��
A.190��200
B.9��9
C.15��9
D.185��200